【算法导论】计数排序

比较排序：通过元素间的比较对序列进行排序的算法称为比较排序。

常见的比较排序算法有：冒泡排序法、插入排序法、合并排序法、快速排序法，堆排序法等等。任何比较排序法在最坏情况下的时间复杂度为$O(nlogn)$。因此，合并排序和堆排序是渐进最优的。

非比较排序：用非比较的方法来进行排序的算法。

常见的非比较排序算法有：计数排序法、基数排序法、桶排序法。它们都是以线性时间运行的。由于是非比较的，因此下界$O(nlogn)$对它们是不适用的。

下面来讨论计数排序：

前提假设：序列的值域在$0$到$k$之间。

时间复杂度：$O(n)$

基本思想：对于序列中的每一个元素，计算得到小于该元素的元素个数，从而确定了该元素在最终输出元素的位置。

从下图中可以了解算法的过程（其中A数组是原始序列，B数组为最终序列，C数组为临时辅助序列。）：

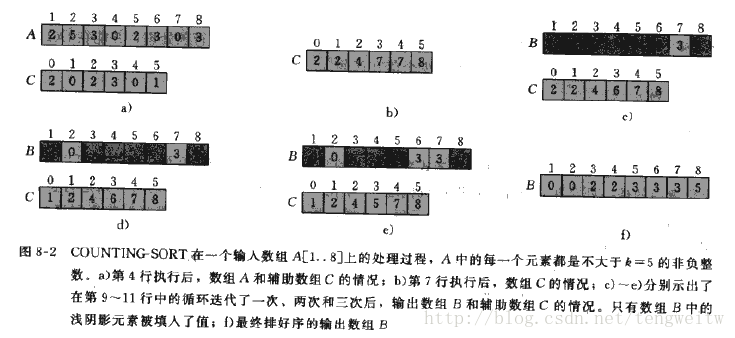
注：黑色方框看不清不要紧，代表的是B数组还没有填充的空间

具体的实现如下：

#include<stdio.h>

void CountSort(int* arrayA,int* arrayB,int* arrayC,int n,int k);

void main()
{
	int arrayA[8]={2,5,3,0,2,3,0,3};
	int arrayB[8]={0};
	int n=sizeof(arrayA)/sizeof(int);
	int k=5;//k为数组中的最大值
	int arrayC[6]={0};

	CountSort(arrayA,arrayB,arrayC,n,k);

	for(int i=0;i<n;i++)
		printf("%d ",arrayB[i]);
	printf("\n");
}

/****************************************\
函数功能：进行非比较的计数排序
输入：数组A、B、C（注意A　B长度相同，与C不一定相同）
输出：无
\****************************************/
void CountSort(int* arrayA,int* arrayB,int* arrayC,int n,int k)
{
	for(int i=0;i<=k;i++)
		arrayC[i]=0;
	for(int j=0;j<n;j++)
		arrayC[arrayA[j]]=arrayC[arrayA[j]]+1;
	for(int i=1;i<=k;i++)
		arrayC[i]=arrayC[i]+arrayC[i-1];
	
	for(int j=n-1;j>=0;j--)
	{
		arrayB[arrayC[arrayA[j]]-1]=arrayA[j];
		arrayC[arrayA[j]]=arrayC[arrayA[j]]-1;
	}

}